ECCO Adjoint & State Estimation
Let’s examine some key concepts related to the most fundamental application of the adjoint for ECCO: state estimation or optimization.
Forward model uses computer code (i.e., algorithms) to simulate changing conditions in a forward direction, for example ocean currents moving heat over time (click to see an example).
Model – data differences are used to determine the "misfit" between the forward model's calculation and observation data (e.g., ocean temperature measured by an in-water sensor).
Cost function measures how well a forward model's output matches observations (e.g., weighted quadratic function of the model-data differences). It's important to minimize the cost, which can be thought of as computation time.
Control variables have values that are subject to change. Examples include initial conditions or boundary conditions. Control variables can be adjusted to change the output of a forward model.
Adjoint models can be used to adjust control variables and reduce model-data differences. Not only that, adjoint solutions can provide a measure of sensitivity of the cost function to the physical variables of the system. The adjoint is used to calculate the gradient of the cost function (see next) with respect to the control variables.
Gradient of the cost function is important information because the ECCO model is nonlinear and has billions of variables! Thus, iterative searches for the optimal solution (i.e., minimized cost function) need directional information – e.g., which way is downhill?
Now that we understand the various components of the optimization problem, let's see how they fit together in a high-level conceptual diagram.
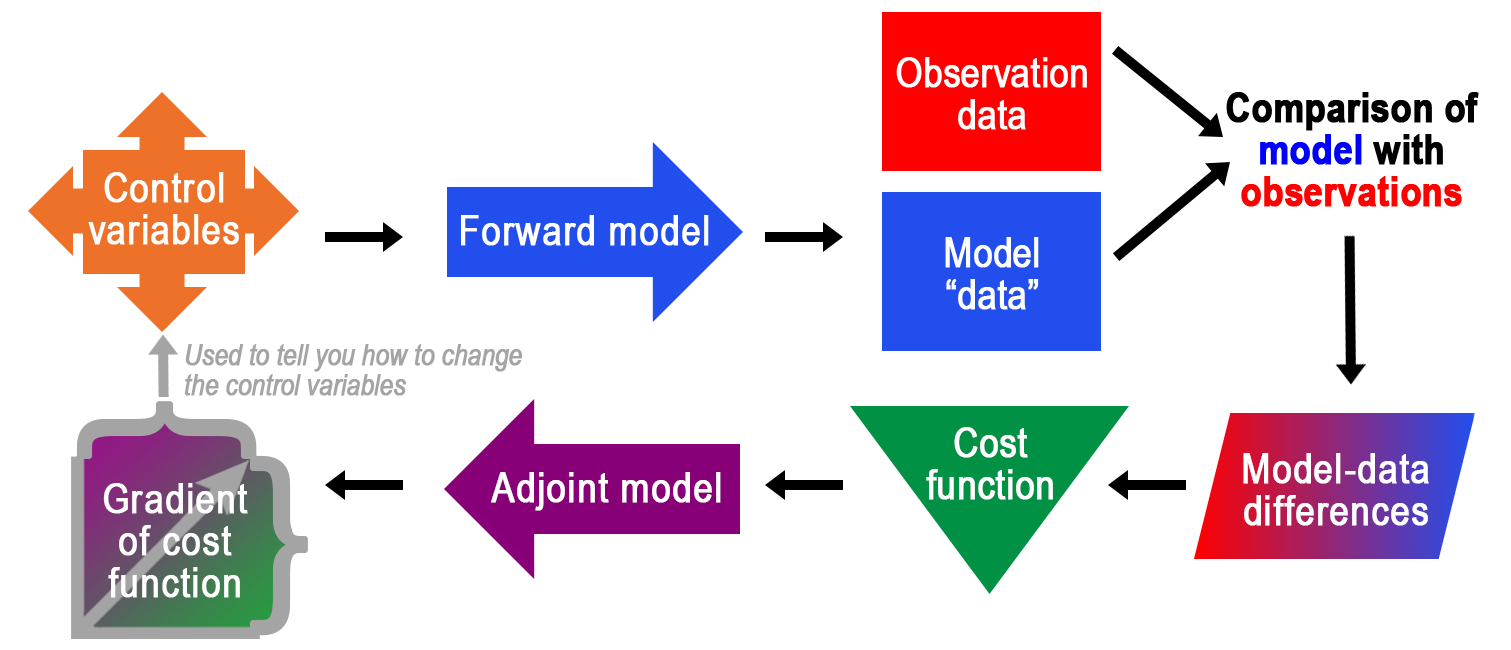
Control variables set the stage for the forward model run. Model "data" (i.e., output) is compared to its real-world counterpart, observation data. Differences between the model and observation data are calculated as a key part of the cost function. Minimizing the cost function is achieved by analyzing its gradients, which are provided by the adjoint model.

